Many skills can help you make better decisions as a domain name investor. One of them is quantitative decision making. While probability can never firmly tell you what to do, it can help make better decisions in some cases.
Applied probability can be used to help answer questions such as how many domains will I probably sell this year, should this domain name be renewed, and whether it is better to renew names in advance of a forthcoming price increase.
Basic Ideas
A probability is a numerical estimate of the chance of something happening. For example, if you roll a normal dice, unless it is rigged in some way, the probability of any particular number being rolled 1 chance in 6.
Normally we express probability on a scale from 0 to 1, with 0 meaning no chance that result will happen, and 1 meaning it is sure to happen. In the dice example, the probability of each number would be about 0.167.
Sometimes probabilities are expressed as percentages, from 0 to 100%, rather than from 0 to 1.
If we go back to the dice example, if we roll it twice, the odds of getting 2 followed by another 2 will be about (1/6)*(1/6), or one chance in 36. That is because the events, for a fair dice, are independent.
It is important to realize that probabilities are not always independent though. For example, the probability of a domain name in a certain sector selling, and the probability of a high sales price, are probably related. If demand for a niche or sector goes up, the chance of a name selling and its price, both increase.
A probability value may change with time. For example, the probability of a metaverse domain name selling 10 years ago was probably less than this year. Some sectors that were hot a few years ago are much less active in domain name sales now.
If you want to read more about probability, the Wikipedia entry on probability is well written.
The Sell-Through Rate, STR
The sell-through rate (STR). STR is simply the number of sales during a 12 month period divided by the average number of names in your portfolio during that year.
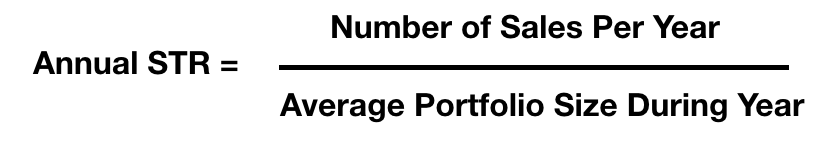
If you have a substantial portfolio, and have been investing in domain names for a number of years, you can calculate your annual sell-through rate (STR) each year.
Many include only sales above some price point in calculating their STR.
The STR is not a probability, but the probability of selling a domain name during a year is expected to be similar to your annual STR, unless something has changed in your domain investing approach.
As a new investor, you will not have an established personal STR from records from previous years. One approach is to use the domain name selling universe, making the rough assumption that your performance might be equal to the average of all names listed for sale. That is relatively easy to calculate as shown below.
This does not mean that will be your STR. Perhaps you have acquired very strong names, or use effective promotion of your names, and achieve a higher STR. On the other hand, many starting out in domain investing probably have a lower STR than the average. Your personal STR may be higher or lower than the industry average.
Why did I introduce the upper cutoff of $25,000? It has almost no impact at all on the STR, but the cutoff upper price does impact the average price significantly. Those 6-figure and up sales have a huge impact on the average price. But most domain investors, particularly those just starting out, may never have a sale in 6-figures. In fact, many will not even have domain names priced above $25,000, so I thought it best to introduce an upper cutoff price to obtain a more reasonable average sales price.
How Many Domains Will I Probably Sell This Year?
Some promote domain name investing as easy and fast. This leads to unreasonable expectations that names will sell for good return on investment quickly. The reality, for almost all domain name investors, is far different.
Let’s look at it numerically. If you have, say 50 domain names, how many sales can you expect in your first year? It is a pretty easy calculation, simply the probability that any one name sells during a 12 year period times the size of your portfolio.

Since you don’t have an established personal STR yet, I will assume that you are ‘average’ and the probability of one of your names selling is equal to the industry-wide STR calculated above, 0.44%.
Let me stress again this is the industry-wide average number. If there is an important message, it is that you must strive to be better than average to find success in domain name investing. Also, unless you are very lucky, a lot of patience will be needed. It is hard waiting those many months before your first sale.
It should be stressed that while it is interesting to see how your STR compares with the industry average, the true measure of success if whether you are profitable. Some have a personal STR well below the average, but sell at great prices and are profitable. Others will sell at a higher rate than the industry average STR, but at prices, or with acquisition costs, that make them overall unprofitable.
Should I Renew This Domain Name?
We all face the issue of which domain names to renew. If we think about the question in a quantitative fashion, the product of the annual probability of sale for the domain name times the expected net return from a sale of that domain name should be higher than the annual costs to hold the domain name in order for it to make sense to renew.

Note that the net return is your gross sales price minus commissions and other costs, and minus your acquisition cost.
I have not included parking revenue in the calculation. If your domain name earns enough parking revenue to cover renewal costs it of course justifies keeping.
If you have a large portfolio, and have been successful in domaining for some years, you can estimate the values for a domain name with more confidence than if you are just starting out.
I covered some factors to consider when deciding to renew a domain name in How To Decide What Domain Names To Renew.
Renew In Advance?
Verisign is raising the wholesale price on
Let’s quantitatively look at the situation using the annual probability of sale of the name, p. If the name does not sell before the period when the renewal kicks in, you have saved the difference between the current and increased renewal rate. On average, the saving is p times the cost savings. However, there is a chance that the name will sell quickly, and you have wasted the amount spent. In this case, we multiply the current renewal times (1-p) where p has been expressed on the usual 0 to 1 scale. I summarize the two calculations below.
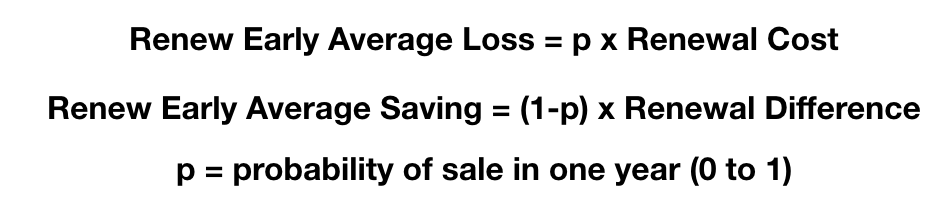
Note this line of thinking does not apply to domain names that you do not feel confident are high enough quality to hold long-term.
Also, even when the calculation shows we save money, on average, by renewing in advance of price increase, only you can say if you have the cashflow to act on it. Even if you do have the funds, you need to ask if this is the best use of money you have. The funds you put into advance renewals will not be available for increasing your portfolio size through acquisitions, which might yield a better return.
Final Thoughts
There are lots of other examples of ways to apply probability ideas to domain name investing decisions.
For example, does it make sense to hold domain names with high premium renewal rates?
What about transferring a name to save on renewal cost, which may make the name not open to fast transfer networks for a period of time, depending on registrar. Do the savings justify the period when your sales chance will be decreased?
An interesting case is for
Perhaps the most important case is using probability estimates to decide whether to accept an offer, or hold out for a higher price, but with some chance the name will never sell.
What about a name you have decided to drop? Does probability suggest it is better to keep the domain name listed at retail price right to the end, or to liquidate for some return?
I may take up some of these other applications in a future article.
I hope you will share interesting ways you use quantitative thinking in your domain name decisions.
Applied probability can be used to help answer questions such as how many domains will I probably sell this year, should this domain name be renewed, and whether it is better to renew names in advance of a forthcoming price increase.
Basic Ideas
A probability is a numerical estimate of the chance of something happening. For example, if you roll a normal dice, unless it is rigged in some way, the probability of any particular number being rolled 1 chance in 6.
Normally we express probability on a scale from 0 to 1, with 0 meaning no chance that result will happen, and 1 meaning it is sure to happen. In the dice example, the probability of each number would be about 0.167.
Sometimes probabilities are expressed as percentages, from 0 to 100%, rather than from 0 to 1.
If we go back to the dice example, if we roll it twice, the odds of getting 2 followed by another 2 will be about (1/6)*(1/6), or one chance in 36. That is because the events, for a fair dice, are independent.
It is important to realize that probabilities are not always independent though. For example, the probability of a domain name in a certain sector selling, and the probability of a high sales price, are probably related. If demand for a niche or sector goes up, the chance of a name selling and its price, both increase.
A probability value may change with time. For example, the probability of a metaverse domain name selling 10 years ago was probably less than this year. Some sectors that were hot a few years ago are much less active in domain name sales now.
If you want to read more about probability, the Wikipedia entry on probability is well written.
The Sell-Through Rate, STR
The sell-through rate (STR). STR is simply the number of sales during a 12 month period divided by the average number of names in your portfolio during that year.
If you have a substantial portfolio, and have been investing in domain names for a number of years, you can calculate your annual sell-through rate (STR) each year.
Many include only sales above some price point in calculating their STR.
EXAMPLE – STR Calculation:
Let’s say someone sets $600 as minimum price for their STR calculation. If they sold 5 domain names above that price during the 12 month period, from a portfolio that ranged from 400 to 600 domain names during the year, averaging 500 names, then the annual STR = 5/500 or 0.01 which is 1%.
The STR is not a probability, but the probability of selling a domain name during a year is expected to be similar to your annual STR, unless something has changed in your domain investing approach.
As a new investor, you will not have an established personal STR from records from previous years. One approach is to use the domain name selling universe, making the rough assumption that your performance might be equal to the average of all names listed for sale. That is relatively easy to calculate as shown below.
EXAMPLE – Industry-Wide STR:
Let’s look just at
.com domain names and the last 5 years to be representative of current conditions. I am going to set the minimum price at $1000 and the maximum at $25,000. See below for a justification on using a maximum.
With the NameBio interface you can readily find the number of sales over the 60-month period, 75,400, and the average price, $3061. But not all sales are in NameBio, since sales at several popular venues are not generally included. If we assume that 25% of the sales of $1000 plus are in NameBio, we can apply an adjustment factor of 4x, making an estimate of 67,860 sales per year.
Using Dofo Advanced search, setting to only
.com and BIN prices of $1000 to $25,000, there were 11,936,067 domain names listed for sale. But not every domain for sale gets in Dofo listings, and also there are some for sale at make offer, or higher prices, that will end up selling within our price range. On the other hand, there are some old listings still on marketplaces that are not truly for sale. Considering all these factors, I applied a net 1.3x correction factor, obtaining 15,516,887 domain names for sale.
Now we can calculate the industry-wide annual
.com STR for sales of $1000 to $25,000 = 67,860 / 15,516,887 = 0.0044 = 0.44%. The average sales price was $3061.This does not mean that will be your STR. Perhaps you have acquired very strong names, or use effective promotion of your names, and achieve a higher STR. On the other hand, many starting out in domain investing probably have a lower STR than the average. Your personal STR may be higher or lower than the industry average.
Why did I introduce the upper cutoff of $25,000? It has almost no impact at all on the STR, but the cutoff upper price does impact the average price significantly. Those 6-figure and up sales have a huge impact on the average price. But most domain investors, particularly those just starting out, may never have a sale in 6-figures. In fact, many will not even have domain names priced above $25,000, so I thought it best to introduce an upper cutoff price to obtain a more reasonable average sales price.
How Many Domains Will I Probably Sell This Year?
Some promote domain name investing as easy and fast. This leads to unreasonable expectations that names will sell for good return on investment quickly. The reality, for almost all domain name investors, is far different.
Let’s look at it numerically. If you have, say 50 domain names, how many sales can you expect in your first year? It is a pretty easy calculation, simply the probability that any one name sells during a 12 year period times the size of your portfolio.
Since you don’t have an established personal STR yet, I will assume that you are ‘average’ and the probability of one of your names selling is equal to the industry-wide STR calculated above, 0.44%.
EXAMPLE How Many Sales From 50 Name Portfolio?
Number of sales in 12 months = probability of sale for one name x number of domain names in portfolio.
Number of annual sales = 0.0044 x 50 = 0.21
This means an investor with a 50 name ‘average’
.com portfolio will have a bit more than 1 chance in 5 of selling a name at the end of one full year, or will, on average, sell one name in a 5 year period.Let me stress again this is the industry-wide average number. If there is an important message, it is that you must strive to be better than average to find success in domain name investing. Also, unless you are very lucky, a lot of patience will be needed. It is hard waiting those many months before your first sale.
It should be stressed that while it is interesting to see how your STR compares with the industry average, the true measure of success if whether you are profitable. Some have a personal STR well below the average, but sell at great prices and are profitable. Others will sell at a higher rate than the industry average STR, but at prices, or with acquisition costs, that make them overall unprofitable.
Should I Renew This Domain Name?
We all face the issue of which domain names to renew. If we think about the question in a quantitative fashion, the product of the annual probability of sale for the domain name times the expected net return from a sale of that domain name should be higher than the annual costs to hold the domain name in order for it to make sense to renew.
EXAMPLE – Should I Renew This Name?
Let’s say the probability of sale of a particular domain name at 0.25%, a bit less than the industry average. If we estimate the net return from a sale, if it happens, based on pricing, expected commission, acquisition cost, etc., would be $1500.
0.0025 x $1500 = $3.75
Therefore it would not make sense to renew this particular domain name, assuming that the renewal fee was $9.00.
Note that the net return is your gross sales price minus commissions and other costs, and minus your acquisition cost.
I have not included parking revenue in the calculation. If your domain name earns enough parking revenue to cover renewal costs it of course justifies keeping.
If you have a large portfolio, and have been successful in domaining for some years, you can estimate the values for a domain name with more confidence than if you are just starting out.
I covered some factors to consider when deciding to renew a domain name in How To Decide What Domain Names To Renew.
Renew In Advance?
Verisign is raising the wholesale price on
.com by another 7% at the end of this month. Some investors are renewing domain names in advance of the price increase. Others argue that if the name sells that is essentially lost money, and only renew near expiration.Let’s quantitatively look at the situation using the annual probability of sale of the name, p. If the name does not sell before the period when the renewal kicks in, you have saved the difference between the current and increased renewal rate. On average, the saving is p times the cost savings. However, there is a chance that the name will sell quickly, and you have wasted the amount spent. In this case, we multiply the current renewal times (1-p) where p has been expressed on the usual 0 to 1 scale. I summarize the two calculations below.
EXAMPLE – Renew In Advance Of Price Increase
You hold a
.com name that you have decided you will want to keep for more than one year if it does not sell. To get a representative cost, I took the 5th best current .com renewal rate at TLD-list, which turned out to be $9.13. With a 7% increase, we expect the new retail renewal to be about $9.77.
Let’s say it is a good name, and you think the probability of sale in any one year is 10%, much better than the industry average. So there is 1 chance in 10 the name sells during the next year before you need that renewal you did in advance. If we multiply $9.13 x 0.10 = $0.91 that would be the probabilistic loss.
Now let’s look at what probability suggests we save by renewing early. There is a probability of 0.90 that we will need to renew the domain name because it did not sell. We save $0.64 by renewing in advance, so that would suggest a $0.64 x 0.90 = $0.58.
Since the saving, for these numbers, is less than the $0.91 calculated earlier, for this high probability of sale domain name it does not make sense to renew in advance.
However, if instead we look at a more typical annual probability of sale, say 1%, the results are different. In this case $9.13 x 0.01 = $0.09 is the average loss by renewing names like this in advance. The expected average saving is now $0.64 x 0.99 = $0.64. Renewing in advance is a no-brainer in this case, if we have the funds and we are sure we want to keep it long term.
Note this line of thinking does not apply to domain names that you do not feel confident are high enough quality to hold long-term.
Also, even when the calculation shows we save money, on average, by renewing in advance of price increase, only you can say if you have the cashflow to act on it. Even if you do have the funds, you need to ask if this is the best use of money you have. The funds you put into advance renewals will not be available for increasing your portfolio size through acquisitions, which might yield a better return.
Final Thoughts
There are lots of other examples of ways to apply probability ideas to domain name investing decisions.
For example, does it make sense to hold domain names with high premium renewal rates?
What about transferring a name to save on renewal cost, which may make the name not open to fast transfer networks for a period of time, depending on registrar. Do the savings justify the period when your sales chance will be decreased?
An interesting case is for
.co and some new extensions where you can get the first year at a discounted rate compared to the regular renewal. The probability argument for this case may suggest the name is worthwhile to hold for one year, but not long term at the higher annual cost.Perhaps the most important case is using probability estimates to decide whether to accept an offer, or hold out for a higher price, but with some chance the name will never sell.
What about a name you have decided to drop? Does probability suggest it is better to keep the domain name listed at retail price right to the end, or to liquidate for some return?
I may take up some of these other applications in a future article.
I hope you will share interesting ways you use quantitative thinking in your domain name decisions.






